☛ Activité préparatoire - Solution

Solution

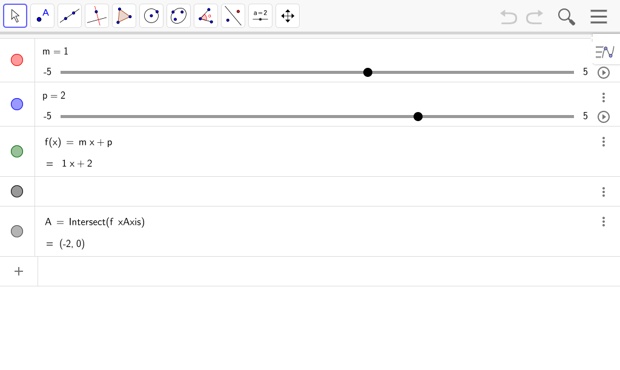
Soit \(m\) et \(p\) deux réels. On considère la fonction affine \(f\) définie sur \(\mathbb{R}\) par \(f(x)=mx+p\).
Voici sa droite représentative \(\mathcal{D}\) dans un repère du plan.

1. Lorsque \(m\) est fixé et \(p\) varie, on observe que la droite \(\mathcal{D}\) effectue des translations verticales.

• Si on augmente la valeur de \(p\), la droite \(\mathcal{D}\) "effectue une translation vers le haut".
• Si on diminue la valeur de \(p\), la droite \(\mathcal{D}\) "effectue une translation vers le bas".
  

2. Lorsque \(p\) est fixé et \(m\) varie, on observe que :

• si \(m>0\), alors on observe que lorsque les valeurs de \(x\) augmentent, les valeurs de \(f(x)\) augmentent également, donc \(f\) semble croissante sur \(\mathbb{R}\) ;
  
• si \(m<0\), alors on observe que lorsque les valeurs de \(x\) augmentent, les valeurs de \(f(x)\) diminuent, donc \(f\) semble décroissante sur \(\mathbb{R}\) ;
• lorsque \(m=0\) alors la droite \(\mathcal{D}\) est parallèle à l'axe des abscisses donc \(f\) semble constante sur \(\mathbb{R}\).
  

3. Dans cette question, on suppose que \(m=0\). 

• Soit \(p=0\) et, dans ce cas, \(f(x)=0\)  a une infinité de solution.
• Soit \(p\neq0\)  et, dans ce cas, \(f(x)=0\) n'a aucune solution.
  

4. Dans cette question on suppose que \(m\neq 0\).
    a.  On constate que la droite \(\mathcal{D}\) ne possède qu'un seul point d'intersection avec l'axe des abscisses. L'équation \(f(x)=0\) semble avoir une unique solution.
    b. Lorsque \(m>0\), la droite \(\mathcal{D}\) ne possède qu'un seul point d'intersection avec l'axe des abscisses.
Notons \(a\) l'abscisse du point d'intersection de \(\mathcal{D}\) avec l'axe des abscisses.
La fonction \(f\) semble négative sur \(]-\infty ; a]\) et positive sur \([a;+\infty[\).
Lorsque \(m<0\), la droite \(\mathcal{D}\) ne possède qu'un seul point d'intersection avec l'axe des abscisses.
Notons \(a\) l'abscisse du point d'intersection de \(\mathcal{D}\) avec l'axe des abscisses.
La fonction \(f\) semble positive sur \(]-\infty ; a]\) et négative sur  \([a;+\infty[\).